Bài 3. Tích của vecto với một số Bài Luyện tập, trắc nghiệm và tự luận

Câu 1 (TCBL10-20670)

Cho hai điểm phân biệt A và B. Tìm điểm K sao cho:

\(3\overrightarrow{KA}+2\overrightarrow{KB}=\overrightarrow{0}\)

K là trung điểm của AB K nằm trên đoạn AB và \(\frac{KA}{KB}=\frac{2}{3}\) K nằm trên đoạn AB và \(\frac{KA}{KB}=\frac{3}{2}\) K trùng với A hoặc B

Câu 2 (TCBL10-20671)

Cho tam giác đều ABC có G là trọng tâm và M là một điểm tùy ý trong tam giác. Gọi D, E, F lần lượt là chân đường vuông góc hạ từ M xuống BC, AC, AB.

Hãy tính tổng \(\overrightarrow{MD}+\overrightarrow{ME}+\overrightarrow{MF}\) theo \(\overrightarrow{MG}\).

\(\overrightarrow{MD}+\overrightarrow{ME}+\overrightarrow{MF}=\frac{3}{2}\overrightarrow{MG}\) \(\overrightarrow{MD}+\overrightarrow{ME}+\overrightarrow{MF}=\overrightarrow{MG}\) \(\overrightarrow{MD}+\overrightarrow{ME}+\overrightarrow{MF}=3\overrightarrow{MG}\) \(\overrightarrow{MD}+\overrightarrow{ME}+\overrightarrow{MF}=\frac{2}{3}\overrightarrow{MG}\)

Câu 3 (TCBL10-20672)

Gọi M và N là trung điểm của các cạnh AB và CD của tứ giác ABCD. Biết rằng \(MN=4cm\)

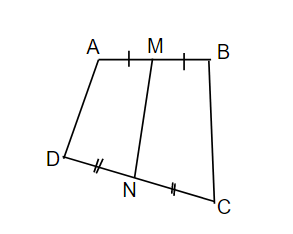
Tính độ dài vecto \(\overrightarrow{AC}+\overrightarrow{BD}+\overrightarrow{BC}+\overrightarrow{AD}\)

1cm 5cm 12cm 16cm

Câu 4 (TCBL10-20673)

Cho tam giác ABC. Xác định vị trí của điểm M sao cho \(\overrightarrow{MA}+2.\overrightarrow{MB}+\overrightarrow{MC}=\overrightarrow{0}\) ?

M trùng với trọng tâm G của tam giác ABC M là trung điểm của trung tuyến kẻ từ đỉnh A M là trung điểm của trung tuyến kẻ từ đỉnh B. M là trung điểm của cạnh AB.

Câu 5 (TCBL10-20674)

Cho tam giác ABC. Đặt \(\overrightarrow{a}=\overrightarrow{BC}\) , \(\overrightarrow{b}=\overrightarrow{AC}\) . Trong các cặp vectơ sau đây, cặp vecto nào sau cùng phương?

\(2\overrightarrow{a}+\overrightarrow{b}\) và \(\overrightarrow{a}+2\overrightarrow{b}\) \(\overrightarrow{a}-2\overrightarrow{b}\) và \(2\overrightarrow{a}-\overrightarrow{b}\) \(5\overrightarrow{a}+\overrightarrow{b}\) và \(-10\overrightarrow{a}-2\overrightarrow{b}\) \(\overrightarrow{a}+\overrightarrow{b}\) và \(\overrightarrow{a}-\overrightarrow{b}\)

Câu 6 (TCBL10-20675)

Cho hình chữ nhật ABCD. Gọi I và K lần lượt là trung điểm của BC, CD. Trong các khẳng định sau, khẳng định nào đúng ?

\(\overrightarrow{AI}+\overrightarrow{AK}=2\overrightarrow{AC}\) \(\overrightarrow{AI}+\overrightarrow{AK}=\overrightarrow{AB}+\overrightarrow{AD}\) \(\overrightarrow{AI}+\overrightarrow{AK}=\overrightarrow{IK}\) \(\overrightarrow{AI}+\overrightarrow{AK}=\frac{3}{2}\overrightarrow{AC}\)

Câu 7 (TCBL10-20676)

Cho tam giác ABC. Biết AB = 8; AC = 9; BC = 11. M là trung điểm của BC, N là điểm trên đoạn AC sao cho \(AN=x\left(0< x< 9\right)\). Hãy khai triển \(\overrightarrow{MN}\) qua \(\overrightarrow{c}=\overrightarrow{AC},\overrightarrow{b}=\overrightarrow{AB}\).

\(\overrightarrow{MN}=\left(\dfrac{1}{2}-\dfrac{x}{9}\right)\overrightarrow{c}+\dfrac{1}{2}\overrightarrow{b}\) \(\overrightarrow{MN}=\left(-\dfrac{x}{9}+\dfrac{1}{2}\right)\overrightarrow{c}-\dfrac{1}{2}\overrightarrow{b}\) \(\overrightarrow{MN}=\left(\dfrac{x}{9}+\dfrac{1}{2}\right)\overrightarrow{c}-\dfrac{1}{2}\overrightarrow{b}\) \(\overrightarrow{MN}=\left(\dfrac{x}{9}-\dfrac{1}{2}\right)\overrightarrow{c}-\dfrac{1}{2}\overrightarrow{b}\)

Câu 8 (TCBL10-20677)

Cho tam giác ABC và một điểm M tùy ý. Hãy tính giá trị biểu thức \(2\overrightarrow{MA}+\overrightarrow{MB}-3\overrightarrow{MC}\) theo \(\overrightarrow{a}=\overrightarrow{CA}\) và \(\overrightarrow{b}=\overrightarrow{CB}\) .

\(2\overrightarrow{MA}+\overrightarrow{MB}-3\overrightarrow{MC}=-\overrightarrow{a}-2.\overrightarrow{b}\) \(2\overrightarrow{MA}+\overrightarrow{MB}-3\overrightarrow{MC}=-2.\overrightarrow{a}-\overrightarrow{b}\) \(2\overrightarrow{MA}+\overrightarrow{MB}-3\overrightarrow{MC}=2.\overrightarrow{a}+\overrightarrow{b}\) \(2\overrightarrow{MA}+\overrightarrow{MB}-3\overrightarrow{MC}=2.\overrightarrow{b}-\overrightarrow{a}\)

Câu 9 (TCBL10-20678)

Cho tam giác ABC. Gọi I và J là hai điểm xác định bởi

\(\overrightarrow{IA}=2\overrightarrow{IB};3\overrightarrow{JA}=2\overrightarrow{JC}=\overrightarrow{0}\)

Hãy tính \(\overrightarrow{IJ}\) theo các vecto \(\overrightarrow{b}=\overrightarrow{AB},\) \(\overrightarrow{c}=\overrightarrow{AC}\).

\(\overrightarrow{IJ}=\dfrac{2}{5}\overrightarrow{b}-2.\overrightarrow{c}\) \(\overrightarrow{IJ}=\dfrac{2}{5}\overrightarrow{c}-2.\overrightarrow{b}\) \(\overrightarrow{IJ}=\dfrac{5}{2}\overrightarrow{c}-2\overrightarrow{b}\) \(\overrightarrow{IJ}=\dfrac{5}{2}.\overrightarrow{b}-2.\overrightarrow{c}\)

Câu 10 (TCBL10-20679)

Cho tam giác ABC. Gọi I là điểm xác định bởi \(\overrightarrow{BI}=k\overrightarrow{BC}\left(k\ne1\right)\) . Biểu diễn \(\overrightarrow{AI}\) qua hai vec to \(\overrightarrow{AB},\overrightarrow{AC}\).

\(\overrightarrow{AI}=\left(k-1\right)\overrightarrow{AB}-k\overrightarrow{AC}\) \(\overrightarrow{AI}=\left(1-k\right)\overrightarrow{AB}+k\overrightarrow{AC}\) \(\overrightarrow{AI}=\left(1+k\right)\overrightarrow{AB}-k\overrightarrow{AC}\) \(\overrightarrow{AI}=\left(1+k\right)\overrightarrow{AB}+k\overrightarrow{AC}\)

Câu 11 (TCBL10-20680)

Cho tam giác ABC, N là điểm xác định bởi \(\overrightarrow{CN}=\frac{1}{2}\overrightarrow{BC}\); G là trọng tâm của tam giác ABC. Hãy biểu diễn \(\overrightarrow{AC}\) theo \(\overrightarrow{AG}\) và \(\overrightarrow{AN}\) .

\(\overrightarrow{AC}=\frac{2}{3}\overrightarrow{AG}+\frac{1}{2}\overrightarrow{AN}\) \(\overrightarrow{AC}=\frac{4}{3}\overrightarrow{AG}-\frac{1}{2}\overrightarrow{AN}\) \(\overrightarrow{AC}=\frac{3}{4}\overrightarrow{AG}+\frac{1}{2}\overrightarrow{AN}\) \(\overrightarrow{AC}=\frac{3}{4}\overrightarrow{AG}-\frac{1}{2}\overrightarrow{AN}\)

Câu 12 (TCBL10-20681)

Cho tam giác đều ABC, tâm O. Kí hiệu M là một điểm bất kì trong tam giác. Hình chiếu vuông góc của M xuống 3 cạnh của tam giác là D, E, F. Tính tổng \(\overrightarrow{MD}+\overrightarrow{ME}+\overrightarrow{MF}\) theo \(\overrightarrow{MO}\) .

\(\overrightarrow{MD}+\overrightarrow{ME}+\overrightarrow{MF}=\frac{1}{2}\overrightarrow{MO}\) \(\overrightarrow{MD}+\overrightarrow{ME}+\overrightarrow{MF}=\frac{2}{3}\overrightarrow{MO}\) \(\overrightarrow{MD}+\overrightarrow{ME}+\overrightarrow{MF}=\frac{3}{4}\overrightarrow{MO}\) \(\overrightarrow{MD}+\overrightarrow{ME}+\overrightarrow{MF}=\frac{3}{2}\overrightarrow{MO}\)

Câu 13 (TCBL10-20682)

Cho tam giác ABC. Xác định vị trí điểm I thỏa mãn điều kiện \(\overrightarrow{IA}+\overrightarrow{IB}-\overrightarrow{IC}=\overrightarrow{0}\)

Trung điểm AB Trọng tâm của tam giác ABC Đỉnh I của hình bình hành ACBI Đỉnh I của hình bình hành ABCI

Câu 14 (TCBL10-20683)

Cho tam giác ABC. Gọi G là trọng tâm tam giác; H là điểm đối xứng của B qua G; M là trung điểm BC. Hãy biểu diễn \(\overrightarrow{MH}\) qua hai vecto \(\overrightarrow{AB}=\overrightarrow{a};\overrightarrow{AC}=\overrightarrow{b}\).

\(\overrightarrow{MH}=\frac{\overrightarrow{b}-5\overrightarrow{a}}{2}\) \(\overrightarrow{MH}=\frac{\overrightarrow{b}-5\overrightarrow{a}}{4}\) \(\overrightarrow{MH}=\frac{\overrightarrow{b}-5\overrightarrow{a}}{6}\) \(\overrightarrow{MH}=\frac{\overrightarrow{b}-5\overrightarrow{a}}{8}\)

Câu 15 (TCBL10-20684)

Cho tam giác ABC. Gọi M là điểm trên cạnh AB sao cho \(\overrightarrow{AM}=\dfrac{1}{4}\overrightarrow{AB}\) và N là điểm trên cạnh CB sao cho

\(\overrightarrow{CN}=\dfrac{3}{5}\overrightarrow{CB}\) . Hãy biểu diễn vecto \(\overrightarrow{MN}\) qua hai vecto \(\overrightarrow{CB}=\overrightarrow{b},\overrightarrow{CA}=\overrightarrow{a}\)

\(\overrightarrow{MN}=\dfrac{3\overrightarrow{b}-11\overrightarrow{a}}{20}\) \(\overrightarrow{MN}=\dfrac{5\overrightarrow{b}-13\overrightarrow{a}}{20}\) \(\overrightarrow{MN}=\dfrac{7\overrightarrow{b}-15\overrightarrow{a}}{20}\) \(\overrightarrow{MN}=\dfrac{9\overrightarrow{b}-17\overrightarrow{a}}{20}\)

Câu 16 (TCBL10-20685)

Cho tam giác ABC. Kí hiệu N là điểm thỏa mãn điều kiện \(\overrightarrow{CN}=\frac{1}{2}\overrightarrow{BC}\) và G là trọng tâm của tam giác ABC. Hãy tính \(\overrightarrow{AC}\) theo \(\overrightarrow{AG,}\overrightarrow{AN}\) .

\(\overrightarrow{AC}=\frac{2}{3}\overrightarrow{AG}+\frac{1}{2}\overrightarrow{AN}\) \(\overrightarrow{AC}=\frac{4}{3}\overrightarrow{AG}-\frac{1}{2}\overrightarrow{AN}\) \(\overrightarrow{AC}=\frac{3}{4}\overrightarrow{AG}-\frac{1}{2}\overrightarrow{AN}\) \(\overrightarrow{AC}=\frac{3}{4}\overrightarrow{AG}+\frac{1}{2}\overrightarrow{AN}\)

Câu 17 (TCBL10-20686)

Cho tam giác ABC. Gọi M là trung điểm cạnh AB và N là điểm trên cạnh AC sao cho NC = 2NA. Gọi K là trung điểm của đoạn MN. Đặt \(\overrightarrow{AB}=\overrightarrow{b};\overrightarrow{AC}=\overrightarrow{c}\) . Hãy khai triển vecto \(\overrightarrow{AK}\) qua \(\overrightarrow{b};\overrightarrow{c}\).

\(\overrightarrow{AK}=\dfrac{1}{4}\overrightarrow{b}+\dfrac{1}{6}\overrightarrow{c}\) \(\overrightarrow{AK}=\dfrac{1}{4}\overrightarrow{b}-\dfrac{1}{6}\overrightarrow{c}\) \(\overrightarrow{AK}=\dfrac{1}{6}\overrightarrow{b}+\dfrac{1}{4}\overrightarrow{c}\) \(\overrightarrow{AK}=\dfrac{1}{6}\overrightarrow{b}-\dfrac{1}{4}\overrightarrow{c}\)

Câu 18 (TCBL10-20687)

Cho tam giác ABC với trọng tâm G. Gọi N là điểm cho bởi \(\overrightarrow{CN}=\dfrac{1}{2}\overrightarrow{BC}\). Hãy tính \(\overrightarrow{AC}\) theo hai vecto \(\overrightarrow{AG},\overrightarrow{AN}\).

\(\dfrac{1}{4}\overrightarrow{AG}+\dfrac{3}{2}\overrightarrow{AN}\) \(\dfrac{3}{4}\overrightarrow{AG}+\dfrac{1}{2}\overrightarrow{AN}\) \(-\dfrac{3}{4}\overrightarrow{AG}+\dfrac{1}{2}\overrightarrow{AN}\) \(\dfrac{3}{4}\overrightarrow{AG}-\dfrac{1}{2}\overrightarrow{AN}\)

Câu 19 (TCBL10-20688)

Cho tam giác ABC; M là một điểm tùy ý. Trong các khẳng định sau, khẳng định nào đúng?

\(2\overrightarrow{MA}+\overrightarrow{MB}-3\overrightarrow{MC}=\overrightarrow{AC}+2\overrightarrow{BC}\) \(2\overrightarrow{MA}+\overrightarrow{MB}-3\overrightarrow{MC}=2\overrightarrow{CA}+\overrightarrow{CB}\) \(2\overrightarrow{MA}+\overrightarrow{MB}-3\overrightarrow{MC}=2\overrightarrow{CB}-\overrightarrow{CA}\) \(2\overrightarrow{MA}+\overrightarrow{MB}-3\overrightarrow{MC}=2\overrightarrow{AC}+\overrightarrow{BC}\)

Câu 20 (TCBL10-20689)

Cho tam giác ABC. M là một điểm trên cạnh BC sao cho \(\overrightarrow{BM}=\dfrac{1}{4}\overrightarrow{BC}\). Hãy khai triển vecto \(\overrightarrow{AM}\) qua \(\overrightarrow{AB},\overrightarrow{AC}\).

\(\overrightarrow{AM}=\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AC}\) \(\overrightarrow{AM}=\dfrac{1}{4}\overrightarrow{AB}+\dfrac{3}{4}\overrightarrow{AC}\) \(\overrightarrow{AM}=\dfrac{3}{4}\overrightarrow{AB}+\dfrac{1}{4}\overrightarrow{AC}\) \(\overrightarrow{AM}=\dfrac{1}{4}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AC}\)

Câu 21 (TCBL10-20690)

Cho tam giác ABC. M là một điểm trên cạnh BC sao cho \(\overrightarrow{BM}=\dfrac{1}{4}\overrightarrow{BC}\). Hãy khai triển vecto \(\overrightarrow{AM}\) qua \(\overrightarrow{AB},\overrightarrow{AC}\).

\(\overrightarrow{AM}=\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AC}\) \(\overrightarrow{AM}=\dfrac{1}{4}\overrightarrow{AB}+\dfrac{3}{4}\overrightarrow{AC}\) \(\overrightarrow{AM}=\dfrac{3}{4}\overrightarrow{AB}+\dfrac{1}{4}\overrightarrow{AC}\) \(\overrightarrow{AM}=\dfrac{1}{4}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AC}\)

Bài 3. Tích của vecto với một số Bài Luyện tập, trắc nghiệm và tự luận - Toán lớp 10

Bài 3. Tích của vecto với một số Bài Luyện tập, trắc nghiệm và tự luận - Toán lớp 10

Luyện tập, Trắc Nhiệm: Bài 3. Tích của vecto với một số

Câu Đúng

Điểm

Lưu câu hỏi

Trụ sở chính:

Chi nhánh TP.Hồ Chí Minh:

Chi nhánh TP.Đà Nẵng:

Chi nhánh TP.Hải Phòng: