Luyện tập, Trắc Nhiệm: Luyện tập Định nghĩa và ý nghĩa của đạo hàm

Cho hàm số \(y=f\left(x\right)=\begin{cases}\dfrac{x^2}{2};\left(x\le1\right)\\ax+b;\left(x>1\right)\end{cases}\)

Tìm  các giá trị của a và b để hàm số có đạo hàm tại \(x=1\).

Cho hàm số \(y=f\left(x\right)=\begin{cases}x^2;\left(x\le2\right)\\-\frac{x^2}{2}+bx+c;\left(x>2\right)\end{cases}\)

Tìm các cặp số \(b,c\) để hàm số có đạo hàm tại x = 2.

Cho hàm số \(y=f\left(x\right)=\begin{cases}ux^2+vx+1;\left(x\ge0\right)\\\left(u+x\right)e^{-vx};\left(x< 0\right)\end{cases}\)

Tìm giá trị thích hợp của u và v để hàm số này có đạo hàm tại x = 0.

Cho hàm số \(y=f\left(x\right)=\begin{cases}\frac{2-\sqrt{4-x}}{x};\left(x\ne0\right)\\\frac{1}{4};\left(x=0\right)\end{cases}\)

Tính \(f'\left(0\right)\)

Cho hàm số \(y=f\left(x\right)=x^2+5x+4\) có đồ thị (P). Tìm phương trình các tiếp tuyến của (P) tại các giao điểm của (P) với trục hoành.

Một đường thẳng (d) cắt đồ thị (P) của hàm số \(y=3x^2-5x+5\) tại \(A\left(2;a\right)\) và \(B\left(b;3\right)\). Tìm hệ số góc của đường thẳng (d).

Cho (P) là đồ thị của hàm số \(y=f\left(x\right)=x^2-2x+3\). Tiếp tuyến của (P) song song với đường thẳng \(4x-2y+5=0\) là đường thẳng có phương trình nào trong số các phương trình dưới đây:

Hàm số  \(y=f\left(x\right)=3x^2-2x+5\) có đồ thị là (P) . Đường thẳng nào trong các đường thẳng cho dưới đây là một tiếp tuyến của (P)  vuông góc với đường thẳng \(x+4y+1=0\) ?

Hàm số \(y=f\left(x\right)=x^2-5x-8\) có đồ thị là (P). Đường thẳng \(y=3x+m\) tiếp xúc với (P), tìm tọa độ tiếp điểm.

Cho hàm số \(y=f\left(x\right)=\dfrac{x^2}{4}-x+1\). Từ điểm \(M\left(2;-1\right)\) có thể kẻ đến đồ thị (P) của hàm số hai tiếp tuyến phân biệt. Viết phương trình hai tiếp tuyến đó.

Cho hàm số \(y=f\left(x\right)=-\dfrac{x^2}{2}+2x+1\) có đồ thị (P) và đường thẳng (d) có phương trình \(y=kx\). Tìm tất cả các giá trị của k để (d) và  (P)  cắt nhau tại hai điểm phân biệt và các tiếp tuyến tại hai giao điểm này  vuông góc nhau.

Gọi (C) là đồ thị của hàm số \(y=f\left(x\right)=-\dfrac{x^3}{3}-2x^2-3x+1\). Có hai tiếp tuyến của (C) cùng có hệ số góc bằng \(\frac{3}{4}\). Tìm phương trình hai tiếp tuyến đó.

Một đường thẳng cắt đồ thị (P) của hàm số \(y=f\left(x\right)=2x^2-3x+5\) tại\(A\left(2;a\right),B\left(b;10\right)\). Tiếp tuyến của (P) song song với đường thẳng đã cho có hệ số góc bằng bao nhiêu?

Gọi (P) là đồ thị của hàm số \(y=f\left(x\right)=\dfrac{x^2}{2}+4x+4\).Tìm phương trình tiếp tuyến của (P) vuông góc với đường thẳng \(x+2y-2=0\).

Cho hàm số \(y=f\left(x\right)=2x^3+3x^2-4x+5\) có đồ thị là (C). Trong số các tiếp tuyến của (C), tiếp tuyến nào có hệ số góc nhỏ nhất?

Cho hàm số \(y=f\left(x\right)=x^3-3x^2\) có đồ thị là (C). Các đường thẳng nào trong các đường thẳng sau đây là những tiếp tuyến của (C) ?

                       \(\left(d_1\right):y=9x+5\); \(\left(d_2\right):y=9x-5\); \(\left(d_3\right):y=9x+27\); \(\left(d_4\right):y=9x-27\)

Cho  bốn đường thẳng  \(\left(d_1\right):y=-8x-3\); \(\left(d_2\right):y=-8x+3\); \(\left(d_3\right):y=8x-3\); \(\left(d_4\right):y=8x+3\)

Cặp đường thẳng nào trong các cặp đường thẳng sau là các tiếp tuyến tại hai \(A\left(1;-5\right)\) và \(B\left(-1;5\right)\) của đồ thị  \(y=f\left(x\right)=x^4-6x^2\) ? 

Tính hệ số góc tiếp tuyến của đồ thị hàm số \(y=\dfrac{x+1}{x-1}\) tại điểm có tung độ bằng 2 .

Một vật rơi tự do theo phương trình \(s=\dfrac{1}{2}gt^2\), trong đó \(g\approx9,8\) (m/\(s^2\) ) là gia tốc trọng trường. Tìm vận tốc tức thời của chuyển động tại thời điểm \(t=10\left(s\right)\)

Cho hàm số \(y=f\left(x\right)\), biết \(\lim\limits_{x\rightarrow+\infty}f\left(x\right)=+\infty;\lim\limits_{x\rightarrow-\infty}f\left(x\right)=-\infty\)

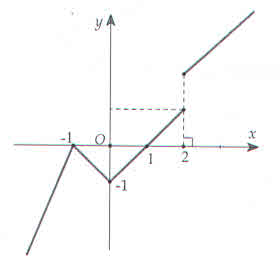
Có bao nhiêu điểm mà tại đấy hàm số không có đạo hàm?

​

Viết phương trình tiếp tuyến của \(\left(C\right):y=x^2\) tại điểm \(M\left(-1;1\right)\).

Tính hệ số góc của tiếp tuyến với đồ thị hàm số \(y=x^3+2017\) tại điểm có hoành độ \(x=-2\):

Điện lượng \(Q\) truyền trong dây dẫn là một hàm số theo thời gian \(t\),  kí hiệu là \(Q=Q\left(t\right)\) và cường độ tức thời của dòng điện tại thời điểm \(t_0\) kí hiệu là \(I\left(t_0\right)\). Khẳng định nào sau đây đúng ? (giả sử các giới hạn tồn tại hữu hạn) 

Một vật chuyển động xác định bởi phương trình \(s\left(t\right)=t^3-2t^2+4t+1\), trong đó \(t\) tính bằng giây và \(s\left(t\right)\) được tính bằng mét. Tính gia tốc của chuyển động tại thời điểm \(t=2\) .

Một vật chuyển động xác định bởi phương trình \(s\left(t\right)=t^3-3t^2+5t+1\), trong đó t tính bằng giây và s(t) được tính bằng mét. Tính vận tốc chuyển động của vật đó tại thời điểm \(t=3\) .

Một chất điểm A xuất phát từ O, chuyển động thẳng với vận tốc biến thiên theo thời gian bởi quy luật \(v\left(t\right)=\dfrac{1}{180}t^2+\dfrac{11}{18}t\left(m/s\right)\), trong đó t (giây) là khoảng thời gian tính từ lúc A bắt đầu chuyển động. Từ trạng thái nghỉ, một chất điểm B cũng xuất phát từ O, chuyển động thẳng cùng hướng với A nhưng chậm hơn 5 giây so với A và có gia tốc bằng \(a\left(m/s^2\right)\) (a là hằng số). Sau khi B xuất phát được 10 giây thì đuổi kịp A. Vận tốc của B tại thời điểm đuổi kịp A bằng

​

Tính hệ số góc của tiếp tuyến với đồ thị \(y=\sqrt[3]{x-1}\) tại điểm có hoành độ \(x=0.\)

Cho (C) là đồ thị hàm số \(y=f\left(x\right)=\frac{8}{x}.\) Số tiếp tuyến của (C) song song với đường thẳng \(y=-2x+8\) là

Viết phương trình tiếp tuyến của đồ thị \(y=f\left(x\right)=x^3-3x^2+2\) tại điểm \(\left(-1;-2\right).\)

​

Viết phương trình tiếp tuyến của đồ thị \(y=f\left(x\right)=x^4-2x^2\) tại điểm có hoành độ \(x=-2.\)

Viết phương trình tiếp tuyến của đồ thị \(y=f\left(x\right)=\frac{x^2+4x+5}{x+2}\) tại điểm có hoành độ \(x=0.\)

Viết phương trình tiếp tuyến của đồ thị \(y=\frac{2x+1}{x-2}\) biết hệ số góc của tiếp tuyến là \(-5.\)

​

Viết phương trình tiếp tuyến của đồ thị \(y=\sqrt{2x+1}\) biết hệ số góc của tiếp tuyến là \(\frac{1}{3}.\)

Tìm hệ số góc tiếp tuyến với đồ thị \(y=\frac{2-3x}{x-1}\) tại giao điểm của đồ thị với trục hoành.

Đồ thị \(y=x^3-3x\) có bao nhiêu tiếp tuyến song song với đường thẳng \(y=9x-4\)?

Đồ thị hàm số \(y=f\left(x\right)=x^3+3x^2+3x+5\) có bao nhiêu cặp tiếp tuyến vuông góc với nhau?

Cho chuyển động thẳng xác định bởi phương trình \(l=t^3-3t^2,\)trong đó \(t\) tính bằng giây (s) và \(l\) tính bằng mét (m). Trong các khẳng định sau, khẳng định nào đúng?