Ôn tập chương Bài Luyện tập, trắc nghiệm và tự luận

Câu 1 (TCBL11-26835)

Cho hàm số $y=f\left(x\right)$ , xác định trên D, $x_0\in D$ . Kí hiệu $f'\left(x_0\right)$ là đạo hàm của hàm số $y=f\left(x\right)$ tại $x_0$ , khẳng định nào sau đây sai ?

$f'\left(x_0\right)=\lim\limits_{x\rightarrow x_0}\dfrac{f\left(x\right)-f\left(x_0\right)}{x-x_0}$

$f'\left(x_0\right)=\lim\limits_{\Delta x\rightarrow0}\dfrac{f\left(\Delta x+x_0\right)-f\left(x_0\right)}{\Delta x}$

$f'\left(x_0\right)=\lim\limits_{t\rightarrow0}\frac{f\left(t+x_0\right)-f\left(x_0\right)}{t}$

$f'\left(x_0\right)=\lim\limits_{x\rightarrow x_0}\dfrac{f\left(x+x_0\right)-f\left(x_0\right)}{x-x_0}$

Đáp án đúng là

$f'\left(x_0\right)=\lim\limits_{x\rightarrow x_0}\dfrac{f\left(x+x_0\right)-f\left(x_0\right)}{x-x_0}$

(Xem hướng dẫn )

Câu 2 (TCBL11-26836)

Xét ba mệnh đề:

(I) : Hàm số $y=\left|x\right|$ xác định tại $x_0=0$

(II) : Hàm số $y=\left|x\right|$ liên tục tại $x_0=0$

(III) : Hàm số $y=\left|x\right|$ có đạo hàm tại $x_0=0$

Trong các khẳng định sau, khẳng định nào đúng ?

(I) và (II) hiển nhiên đúng; (3) sai vì không tồn tại giới hạn $\lim\limits_{x\rightarrow0}\frac{f\left(x\right)-f\left(0\right)}{x-0}=\lim\limits_{x\rightarrow0}\frac{\left|x\right|}{x}$ không tồn tại. Thật vậy:

$\lim\limits_{x\rightarrow0^+}\frac{\left|x\right|}{x}=\lim\limits_{x\rightarrow0^+}\frac{x}{x}=1$ và $\lim\limits_{x\rightarrow0^-}\frac{\left|x\right|}{x}=\lim\limits_{x\rightarrow0^-}\frac{-x}{x}=-1$ có giá trị khác nhau. Vậy khẳng định đúng là " Chỉ (I) và (II) đúng".

Chỉ I đúng Chỉ II đúng Cả I, II, III đều đúng Chỉ I, II đúng

Câu 3 (TCBL11-26837)

Tính đạo hàm của hàm số $y=4\sqrt{x}$ trên $\left(0;+\infty\right)$ ?

$y'=\dfrac{1}{8\sqrt{x}}$

$y'=\dfrac{1}{2\sqrt{x}}$

$y'=\dfrac{2}{\sqrt{x}}$

$y'=\dfrac{8}{\sqrt{x}}$

Đáp án đúng là

$y'=\dfrac{2}{\sqrt{x}}$

(Xem hướng dẫn )

Câu 4 (TCBL11-26838)

Tính đạo hàm của hàm số $y=2x^5-4x^3+\sqrt{x}+x+2$ trên $\left(0;+\infty\right)$ ?

$y'=10x^4-12x^2+\dfrac{1}{2\sqrt{x}}$

$y'=10x^4-12x^2+\dfrac{1}{2\sqrt{x}}+x+1$

$y'=10x^4-12x^2+\dfrac{1}{2\sqrt{x}}+1$

$y'=10x^4-12x^2+\dfrac{1}{\sqrt{x}}+1$

Đáp án đúng là

$y'=10x^4-12x^2+\dfrac{1}{2\sqrt{x}}+1$

(Xem hướng dẫn )

Câu 5 (TCBL11-26839)

Tính đạo hàm của hàm số $y=4x^2+\left(m+2\right)x+m^3$ ( m là tham số )

$y'=8x^2+m+2+3m^2$

$y'=8x^2+m+2$

$y'=8x+m+2$

$y'=8x+m+2+3m^2$

Đáp án đúng là

$y'=8x+m+2$

(Xem hướng dẫn )

Câu 6 (TCBL11-26840)

Tính đạo hàm của hàm số $y=\dfrac{2x-1}{x+1}$ .

$y'=\dfrac{1}{\left(x+1\right)^2}$

$y'=\dfrac{-3}{\left(x+1\right)^2}$

$y'=\dfrac{3}{\left(x+1\right)^2}$

$y'=\dfrac{3}{x+1}$

Đáp án đúng là

$y'=\dfrac{3}{\left(x+1\right)^2}$

(Xem hướng dẫn )

Câu 7 (TCBL11-26841)

Tính đạo hàm của hàm số $y=3\left(2x+1\right)^5$ .

$y'=15\left(2x+1\right)^4$

$y'=30\left(2x+1\right)^4$

$y'=30\left(2x+1\right)^5$

$y'=5\left(2x+1\right)^4$

Đáp án đúng là

$y'=30\left(2x+1\right)^4$

(Xem hướng dẫn )

Câu 8 (TCBL11-26842)

Cho hàm số $f\left(x\right)=\dfrac{x^3}{3}+\left(m-1\right)x^2+4x-1$

Tập tất cả các giá trị thực của tham số m để $f'\left(x\right)\ge0;\forall x\in R$

$\left(0;2\right)$

$\left[0;2\right]$

$\left(-\infty;0\right)\cup\left(2;+\infty\right)$ (-

$\infty$ ; 0]

$\cup$ [2 ; +

$\infty$ )

Đáp án đúng là

$\left[0;2\right]$

(Xem hướng dẫn )

Câu 9 (TCBL11-26843)

Tìm vi phân của hàm số $y=\sqrt{4x^2+x+1}$ ?

$dy=\dfrac{1}{2\sqrt{4x^2+x+1}}dx$

$dy=\dfrac{4x}{\sqrt{4x^2+x+1}}dx$

$dy=\dfrac{4x+1}{\sqrt{4x^2+x+1}}dx$

$dy=\dfrac{8x+1}{2\sqrt{4x^2+x+1}}dx$

Đáp án đúng là

$dy=\dfrac{8x+1}{2\sqrt{4x^2+x+1}}dx$

(Xem hướng dẫn )

Câu 10 (TCBL11-26844)

Cho đồ thị hàm số $\left(C\right):y=\dfrac{x^3}{3}-2x^2+x-2$

Viết phương trình tiếp tuyến của đồ thị (C) song song với đường thẳng $y=-2x+5$ .

$y=2x-1$

$y=-2x+1$

$y=2x+2$

$y=-2x+2$

Đáp án đúng là

$y=-2x+2$

(Xem hướng dẫn )

Câu 11 (TCBL11-26845)

Cho hàm số $f\left(x\right)=a\cos x+2\sin x-3x+2017$

Tập tất cả các giá trị thực của tham số m để phương trình $f'\left(x\right)=0$ có nghiệm

$\left(0;\sqrt{5}\right)$

$\left[-\sqrt{5};\sqrt{5}\right]$

$\left(-\infty;-\sqrt{5}\right)\cup\left(\sqrt{5};+\infty\right)$ (

$-\infty;-\sqrt{5}$ ]

$\cup$ [

$\sqrt{5};+\infty$ )

Đáp án đúng là

( $-\infty;-\sqrt{5}$ ] $\cup$ [ $\sqrt{5};+\infty$ )

(Xem hướng dẫn )

Câu 12 (TCBL11-26846)

Tìm số gia của hàm số $f\left(x\right)=3x^2+x$ tại điểm $x_0=1$ ứng với số gia $\Delta_x$ của đối số.

$\Delta y=\Delta x\left(3\Delta x+7\right)$

$\Delta y=\Delta x\left(2\Delta x+7\right)$

$\Delta y=\Delta x\left(3\Delta x+1\right)$

$\Delta y=\Delta x\left(4\Delta x+7\right)$

Đáp án đúng là

$\Delta y=\Delta x\left(3\Delta x+7\right)$

(Xem hướng dẫn )

Câu 13 (TCBL11-26847)

Tìm số gia $\Delta y$ của hàm số $y=5x-3$ ứng với số gia $\Delta_x$ tại $x$ .

$5$

$-5\Delta x$

$5\Delta x-6$

$5\Delta x$

Đáp án đúng là

$5\Delta x$

(Xem hướng dẫn )

Câu 14 (TCBL11-26848)

Cho hàm số $f\left(x\right)$ là hàm số xác định trên R, định bởi $f\left(x\right)=x^3$ và $x_0\in R$ . Chọn khẳng định đúng ?

$f'\left(x_0\right)=x^3_0$

$f'\left(x_0\right)=3x_0$

$f'\left(x_0\right)=3x^2_0$

$f'\left(x_0\right)=\dfrac{1}{3}x^2_0$

Đáp án đúng là

$f'\left(x_0\right)=3x^2_0$

(Xem hướng dẫn )

Câu 15 (TCBL11-26849)

Cho hàm số $f\left(x\right)=\left(2x-3\right)^2$ . Tính $f'\left(2\right)$

4 2 - 4 - 2

Câu 16 (TCBL11-26850)

Cho hàm số $y=x^3-3x^2-mx-5$ xác định trên R (m là tham số thực) có đạo hàm $y'$ . Tìm các giá trị của tham số m để $x=-1$ là một nghiệm của phương trình $y'=0$ .

- 1 3 - 9 9

Câu 17 (TCBL11-26851)

Tìm đạo hàm của hàm số $y=\dfrac{2x+1}{x-1}$ .

$y'=\dfrac{2}{\left(x-1\right)^2}$

$y'=\dfrac{-1}{\left(x-1\right)^2}$

$y'=\dfrac{-3}{\left(x-1\right)^2}$

$y'=\dfrac{1}{\left(x-1\right)^2}$

Đáp án đúng là

$y'=\dfrac{-3}{\left(x-1\right)^2}$

(Xem hướng dẫn )

Câu 18 (TCBL11-26852)

Cho hàm số $f\left(x\right)=2\sqrt{x}-\dfrac{2}{x}$ xác định trên $\left(0;+\infty\right)$ . Tính đạo hàm của hàm số $f\left(x\right)$ tại $x=4$ ?

$\dfrac{5}{8}$

$0$

$\dfrac{3}{2}$

$\dfrac{1}{2}$

Đáp án đúng là

$\dfrac{5}{8}$

(Xem hướng dẫn )

Câu 19 (TCBL11-26853)

Tính đạo hàm của hàm số $y=x^2\cos x$ .

$y'=2x\cos x-x^2\sin x$

$y'=2x\cos x+x^2\sin x$

$y'=2x\sin x-x^2\cos x$

$y'=2x\sin x+x^2\cos x$

Đáp án đúng là

$y'=2x\cos x-x^2\sin x$

(Xem hướng dẫn )

Câu 20 (TCBL11-26854)

Cho hàm số $y=\cos3x\sin2x$ . Tính $y'\left(\dfrac{\pi}{3}\right)$ .

$-1$

$-\dfrac{1}{2}$

$\dfrac{1}{2}$

$1$

Đáp án đúng là

$1$

(Xem hướng dẫn )

Câu 21 (TCBL11-26855)

Cho hàm số $f\left(x\right)=\left\{{}\begin{matrix}x^2+2x+1;\left(x\ge0\right)\\2x+1;\left(x< 0\right)\end{matrix}\right.$ . Tính $f'\left(0\right)$ ?

$\dfrac{1}{4}$

$2$

$-2$ Không tồn tại

Đáp án đúng là

$2$

(Xem hướng dẫn )

Câu 22 (TCBL11-26856)

Cho hàm số $f\left(x\right)=\left(m+3\right)\cos x+\left(m-4\right)\sin x-5x+m$

Tìm tất cả các giá trị của tham số thực m để phương trình $f'\left(x\right)=0$ có nghiệm ?

$m\in\left(-1;0\right)$

$m\in\left[0;1\right]$

$m\in$ (

$-\infty;-1$ ]

$\cup$ (

$0;+\infty$ )

$m\in$ (

$-\infty;0$ ]

$\cup$ [1;

$+\infty$ )

Đáp án đúng là

$m\in$ ( $-\infty;0$ ] $\cup$ [1; $+\infty$ )

(Xem hướng dẫn )

Câu 23 (TCBL11-26857)

Cho hàm số $y=f\left(x\right)=3+\dfrac{5}{x};\left(x>0\right)$ . Trong các mệnh đề sau, mệnh đề nào đúng ?

$xy'+y=3$

$xy'+y=0$

$xy'+y+3=0$

$xy'+y-x=3$

Đáp án đúng là

$xy'+y=3$

(Xem hướng dẫn )

Câu 24 (TCBL11-26858)

Tính đạo hàm của hàm số $f\left(x\right)=\dfrac{1}{1-x}$ .

$f'\left(x\right)=\dfrac{1}{\left(1-x\right)^2}$

$f'\left(x\right)=\dfrac{-x}{\left(1-x\right)^2}$

$f'\left(x\right)=\dfrac{-1}{\left(1-x\right)^2}$

$f'\left(x\right)=\dfrac{2}{\left(1-x\right)^2}$

Đáp án đúng là

$f'\left(x\right)=\dfrac{1}{\left(1-x\right)^2}$

(Xem hướng dẫn )

Câu 25 (TCBL11-26859)

Xét các mệnh đề sau :

(I) : Nếu hàm số $y=f\left(x\right)$ liên tục tại $x=x_0$ thì $y=f\left(x\right)$ có đạo hàm tại điểm đó.

(II) : Nếu hàm số $y=f\left(x\right)$ có đạo hàm tại $x=x_0$ thì hàm số đã cho liên tục tại $x=x_0$ .

(III) : Nếu hàm số gián đoạn tại $x=x_0$ thì hàm số không có đạo hàm tại điểm đó.

(IV) : Nếu hàm số không có đạo hàm tại $x=x_0$ thì hàm số không liên tục tại điểm đó.

Trong các mệnh đề trên có bao nhiêu mệnh đề đúng?

$1$

$2$

$3$

$4$

Đáp án đúng là

$2$

(Xem hướng dẫn )

Câu 26 (TCBL11-26860)

Tính đạo hàm của hàm số $y=3x^4+\sqrt{x}+2x+4$ trên $\left(0;+\infty\right)$ ?

$y'=12x^4+\dfrac{1}{2\sqrt{x}}+2$

$y'=12x^3+\dfrac{1}{2\sqrt{x}}+2$

$y'=12x^3-\dfrac{1}{2\sqrt{x}}+2$

$y'=12x^3+\dfrac{1}{2\sqrt{x}}$

Đáp án đúng là

$y'=12x^3+\dfrac{1}{2\sqrt{x}}+2$

(Xem hướng dẫn )

Câu 27 (TCBL11-26861)

Tính đạo hàm của hàm số $y=x^4-\left(m-1\right)x^2+m^2$ ( m là tham số )

$y'=4x^3-\left(m-1\right)x$

$y'=4x^3-2\left(m-1\right)x+2m$

$y'=4x^3-2\left(m-1\right)x$

$y'=4x^3-2\left(m-1\right)$

Đáp án đúng là

$y'=4x^3-2\left(m-1\right)x$

(Xem hướng dẫn )

Câu 28 (TCBL11-26862)

Tính đạo hàm của hàm số $y=\dfrac{2x+1}{x-1}$ .

$y'=\dfrac{1}{\left(x-1\right)^2}$

$y'=\dfrac{-3}{\left(x-1\right)^2}$

$y'=\dfrac{3}{\left(x-1\right)^2}$

$y'=\dfrac{-3}{x-1}$

Đáp án đúng là

$y'=\dfrac{-3}{\left(x-1\right)^2}$

(Xem hướng dẫn )

Câu 29 (TCBL11-26863)

Tính đạo hàm của hàm số $y=2\left(x^2+x+1\right)^3$ .

$y'=6\left(x^2+x+1\right)$

$y'=6\left(2x+1\right)\left(x^2+x+1\right)^2$

$y'=2\left(2x+1\right)\left(x^2+x+1\right)^2$

$y'=6\left(2x+1\right)\left(x^2+x+1\right)^3$

Đáp án đúng là

$y'=6\left(2x+1\right)\left(x^2+x+1\right)^2$

(Xem hướng dẫn )

Câu 30 (TCBL11-26864)

Cho hàm số $f\left(x\right)=x\sqrt{x+1}$ . Tính $f'\left(3\right)$ ?

$f'\left(3\right)=\dfrac{11}{4}$

$f'\left(3\right)=-\dfrac{11}{4}$

$f'\left(3\right)=\dfrac{7}{4}$

$f'\left(3\right)=2$

Đáp án đúng là

$f'\left(3\right)=\dfrac{11}{4}$

(Xem hướng dẫn )

Câu 31 (TCBL11-26865)

Hàm số $y=2\cos x+4x-1$ là đạo hàm của hàm số nào sau đây ?

$f_1\left(x\right)=2\sin x+2x^2$

$f_2\left(x\right)=2\sin x+2x^2-1$

$f_3\left(x\right)=2\sin x+2x^2+x$

$f_4\left(x\right)=2\sin x+2x^2-x-2017$

Đáp án đúng là

$f_4\left(x\right)=2\sin x+2x^2-x-2017$

(Xem hướng dẫn )

Câu 32 (TCBL11-26866)

Cho hàm số $f\left(x\right)=x^4+\left(1-m^2\right)x^2+2017$

Hãy tìm tập tất cả các giá trị thực của tham số m để phương trình $f'\left(x\right)=0$ có 3 nghiệm thực phân biệt .

$\left(-1;1\right)$

$\left[-1;1\right]$

$(-\infty;-1)$

$\cup$

$\left(1;+\infty\right)$ (

$-\infty;-1$ ]

$\cup$ [

$1;+\infty$ )

Đáp án đúng là

$(-\infty;-1)$ $\cup$ $\left(1;+\infty\right)$

(Xem hướng dẫn )

Câu 33 (TCBL11-26867)

Viết phương trình tiếp tuyến với đồ thị hàm số $f\left(x\right)=x^3-2x^2-2$ tại điểm có hoành độ $x_0=-2$ .

$y=4x-8$

$y=20x-16$

$y=20x+22$

$y=20x-22$

Đáp án đúng là

$y=20x+22$

(Xem hướng dẫn )

Câu 34 (TCBL11-26868)

Cho hai hàm số $f\left(x\right)=\sin^4x+\cos^4x$ và $g\left(x\right)=\dfrac{1}{4}\cos4x$ khẳng định nào sau đây sai ?

$f'\left(x\right)=-\sin4x$

$2g'\left(x\right)+2\sin4x=0$

$f'\left(x\right)=g'\left(x\right)$

$f'\left(x\right)-g'\left(x\right)=2\sin4x$

Đáp án đúng là

$f'\left(x\right)-g'\left(x\right)=2\sin4x$

(Xem hướng dẫn )

Câu 35 (TCBL11-26869)

Tìm số gia của hàm số $f\left(x\right)=x^2+1$ tại điểm $x_0=1$ ứng với số gia $\Delta x=1$ ?

$\Delta y=-1$

$\Delta y=-2$

$\Delta y=1$

$\Delta y=3$

Đáp án đúng là

$\Delta y=3$

(Xem hướng dẫn )

Câu 36 (TCBL11-26870)

Cho 4 hàm số có đồ thị cho bởi các hình vẽ sau :

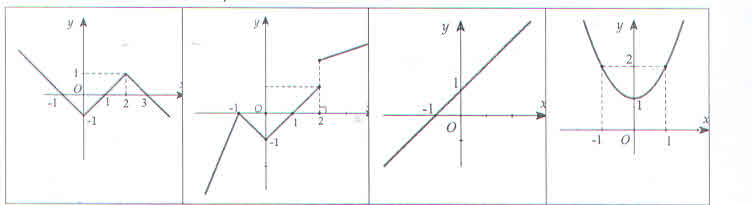
Hỏi có bao nhiêu hàm số có đạo hàm trên $\left(0;+\infty\right)$ ?

1 2 3 4

Ôn tập chương Bài Luyện tập, trắc nghiệm và tự luận - Toán lớp 11

Ôn tập chương Bài Luyện tập, trắc nghiệm và tự luận - Toán lớp 11

Luyện tập, Trắc Nhiệm: Ôn tập chương

Câu Đúng

Điểm

Lưu câu hỏi

Trụ sở chính:

Chi nhánh TP.Hồ Chí Minh:

Chi nhánh TP.Đà Nẵng:

Chi nhánh TP.Hải Phòng: